Funded by NSF CISE Research Initiation Initiative (CRII) Program · Grant No.: CNS 1566579 · Program Manager: M. Mimi McClure

Project Overview

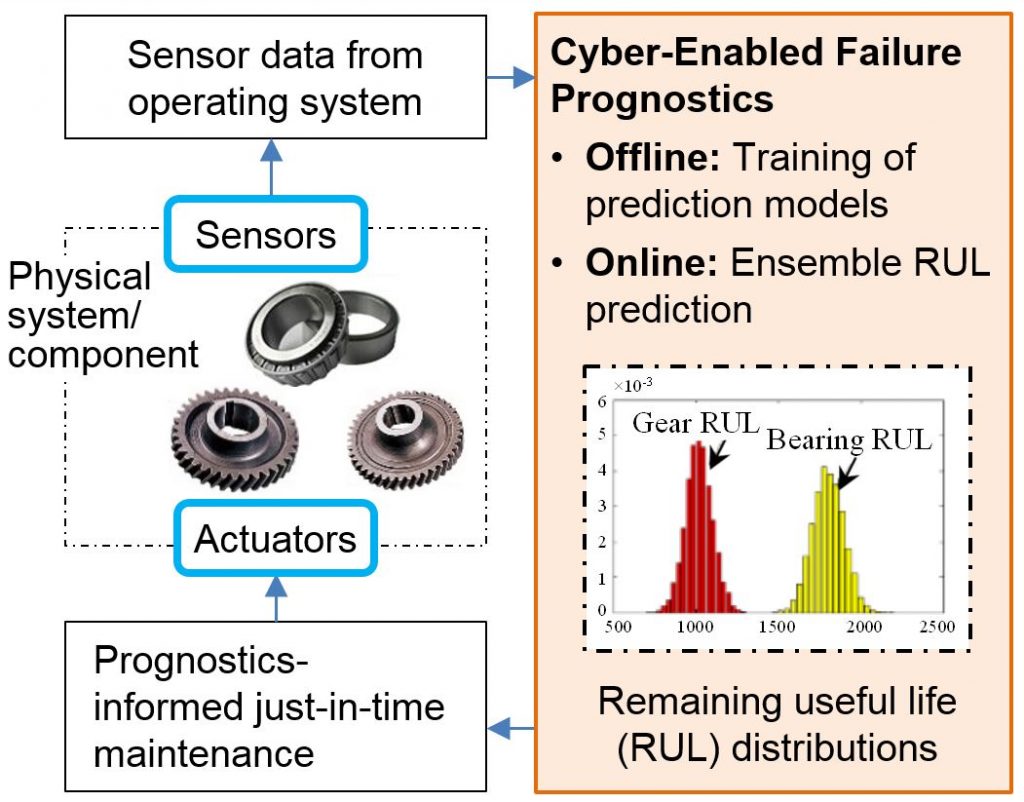
The objective of this project is to develop a novel design platform to improve failure resilience in complex cyber-physical systems (CPSs) by exploiting the synergy between the design and operation of the physical systems. The design platform provides new methods and tools needed to leverage cyber-enabled failure prognostics and prognostics-informed failure recovery (via just-in-time maintenance) for making CPSs failure resilient. We have been working on the two aspects of the design platform: (1) building a “cheap-to-evaluate” metamodel to replace an expensive design model for efficient reliability analysis and model updating; and (2) developing a generic prognostics and health management (PHM) design framework that ensures robust prognostics across different cyber-physical applications. We expect the success of this research to produce major advancements in extending life and durability of CPSs and potentially lead to the development of CPSs that are more reliable and cost-effective than existing systems.

---

Reliability Analysis of Low- to Moderate-Dimensional Physical Systems

The design model of a physical system approximates the relationship between the inputs and outputs of the system. A direct simulation approach to analyzing the reliability of the physical system requires evaluating its design model at a large number of random input samples. However, the design model is often highly complex and time-consuming to evaluate, which may make direct simulation-based reliability analysis prohibitively expensive. One way to address this issue is to build a computationally “cheaper” metamodel that replaces the expensive design model and use the metamodel for reliability analysis.

For physical systems of low to moderate dimensionality (typically < 15), we proposed and implemented a new sequential sampling (or sequential design of experiments) method, named as sequential exploitation-exploration with dynamic trade-off (SEEDT) [1], that employs kriging (or Gaussian process regression) to efficiently build a metamodel and performs Monte Carlo simulation on the metamodel to evaluate the reliability. A critical element of SEEDT is a novel acquisition function, referred to as expected utility, that allows evaluating the utility of a candidate sample point to enhance the accuracy and reduce the uncertainty in the prediction of the limit-state function (LSF). An accurate prediction of the LSF, which separates the safe region from the failure region in the input space, is essential for accurate reliability analysis. As shown in the video below, SEEDT sequentially locates critical sample points in regions of the input space that are highly uncertain and/or close to the LSF. As the number of sample points increases, the accuracy (uncertainty) of the metamodel and its prediction of the LSF increases (decreases) and, as a result, the reliability estimation error gradually decreases, eventually to below an error threshold.

For more information, please see Ref. [1] in the Publications List.

---

Reliability Analysis of High-Dimensional Physical Systems

For physical systems of high dimensionality (typically ≥ 15), the efficiency of kriging diminishes dramatically. This severely limits the application of kriging-based metamodels to reliability analysis of physical systems that involve high dimensions and expensive simulations.

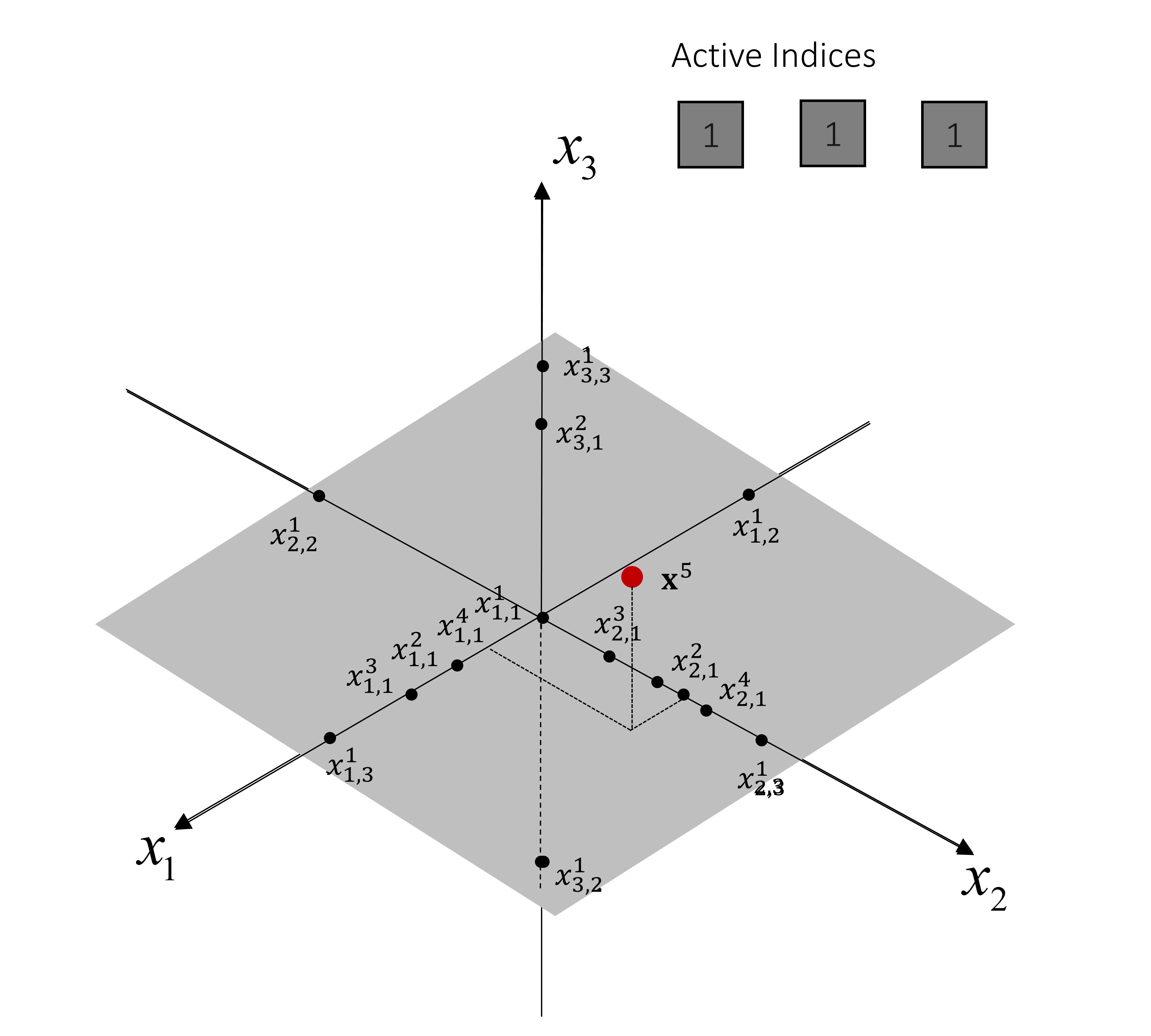
In this work, we created an efficient hybrid of adaptive univariate dimension reduction (UDR) and sequential kriging to alleviate the curse of dimensionality and enable efficient reliability analysis with high-dimensional, computationally expensive design models. This hybrid method, called high-dimensional reliability analysis (HDRA) [2], decomposes the task of metamodel construction for reliability analysis into two sequential steps. In the first step (Step 1), adaptive UDR sequentially locates significant univariate sample points by decomposing the important multivariate points identified by SEEDT (as shown in the video). A UDR-based global metamodel is then constructed based on these univariate sample points. In the second step (Step 2), the global metamodel is used as the trend function in the kriging model, and SEEDT further refines the metamodel by sequentially locating critical multivariate sample points in highly uncertain regions close to the LSF.

For more information, please see Ref. [2] in the Publications List.

---

Real-Time Updating of Strain Map Models of Large-Scale Structures

We also examined the applications of kriging-based metamodeling to build and update, in (close to) real-time, models of unidirectional and additive strain maps for large-scale structural systems [3,4]. We have improved the accuracy and robustness in real-time reconstruction of the strain map models over the state-of-the-art methods developed in the field of structural health monitoring. This improvement was achieved via novel applications of kriging-based metamodeling to solve the problem of inferring the parameters of strain map models from unidirectional and additive strain measurements by dense sensor networks. Such applications contributed to the science of structural health monitoring by being the first studies that investigate the use of kriging-based metamodeling to enable real-time reconstruction of strain map models from measurements of unidirectional and additive strains by dense sensor networks. The video below shows the real-time reconstruction of the strain map of our developed experimental test bench.

For more information, please see Refs. [3,4] in the Publications List.

---

Ensemble Prognostics of Physical System Failures

In this work, we investigated the use of ensemble learning with degradation-dependent weighting to achieve robust cyber-enabled prognostics of physical system failures [5]. Specifically, we have designed and implemented a new ensemble prognostics method that assigns degradation-dependent weights to multiple member prognostics algorithms, and have proved with two engineering case studies that the new method can substantially improve prognostic accuracy and robustness over the existing ensemble prognostics method. 

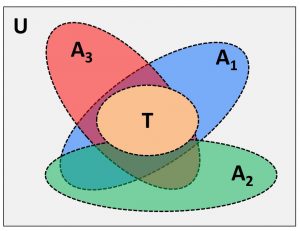
The figure on the right illustrates how a combination of multiple prognostic algorithms expands a correct prognostics region in a testing sample space (U)—it means the prognostic samples obtained under all possible testing conditions. In the figure, T denotes a training sample space, which is a subset of the testing sample space (U). The training sample space encompasses the prognostic samples obtained under all training conditions that are considered. Each individual prognostic algorithm is trained independently with the training samples (T). Since each trained algorithm performs differently, the correct prognostics regions of these algorithms differ from each other (see A₁, A₂, and A₃ in the figure). Should a testing condition fall outside the training sample space, a single prognostic algorithm may not accurately predict the remaining useful life under the testing condition. In contrast, the ensemble approach is more likely to make an accurate prediction because of its expanded region of correct prognostics (≈ A₁ ⊕ A₂ ⊕ A₃). This expansion indicates an improvement in prognostic robustness by using the ensemble since an incorrect prognostics of a testing sample by one prognostic algorithm could be compensated by the correct prognostics of the same sample by another algorithm.

For more information, please see Ref. [5] in the Publications List.

---

Key Outcomes and Achievements

The project has produced seven journal papers published [1-7], one journal paper under review [8], and four conference papers [9-12]. The publication details can be found in the publications list.

In addition, we have developed a novel parallel computing strategy for further improving the computational efficiency of sequential design of experiments when building a kriging metamodel. The new strategy has been demonstrated with a medical device modeling problem through collaboration with Medtronic plc. We are in the process of working with the numerical modeling group at Medtronic to implement this parallel computing strategy on their simulation platform.

---

Publications

1. Sadoughi M., Hu C., MacKenzie C., Eshghi A.T., and Lee S., “Sequential Exploration-Exploitation with Dynamic Trade-off for Efficient Reliability Analysis of Complex Engineered Systems,” Structural and Multidisciplinary Optimization, v57, n1, p235–250, 2018.  [ DOI ]
2. Sadoughi M., Li M., Hu C., MacKenzie C., Eshghi A.T., and Lee S., “A High-Dimensional Reliability Analysis Method for Simulation-Based Design under Uncertainty,” Journal of Mechanical Design, v140, n7, 071401(12), 2018. [ DOI ]
3. Sadoughi M., Downey A., Yan J., Hu C., and Laflamme S., “Reconstruction of Unidirectional Strain Maps via Iterative Signal Fusion for Mesoscale Structures Monitored by a Sensing Skin,” Mechanical Systems and Signal Processing, v112, p401–416, 2018. [ DOI ]
4. Downey A., Sadoughi M., Laflamme S., and Hu C., “Fusion of sensor geometry into additive strain fields measured with sensing skin,” In Press, Smart Materials and Structures, 2018. [ DOI ]
5. Li Z., Wu D., Hu C., and Terpenny J., “An Ensemble Learning-based Prognostic Approach with Degradation-Dependent Weights for Remaining Useful Life Prediction,” In Press, Reliability Engineering and System Safety, https://doi.org/10.1016/j.ress.2017.12.016, 2017. [ DOI ]
6. MacKenzie C., and Hu C., “Decision Making under Uncertainty for Design of Resilient Engineered Systems,” In Press, Reliability Engineering and System Safety, https://doi.org/10.1016/j.ress.2018.05.020, 2018. [ DOI ]
7. Li Z., Jiang Y., Guo Q., Hu C., and Peng Z., “Multi-Dimensional Variational Decomposition for Bearing-Crack Detection in Wind Turbines with Large Driving-Speed Variations,” Renewable Energy, v116 (Part B), p55–73, 2018. [ DOI ]
8. Sadoughi M., Li M., and Hu C., “Multivariate System Reliability Analysis Considering Highly Nonlinear and Dependent Safety Events,” Under Review, Reliability Engineering and System Safety, 2018.
9. Sadoughi M., Li M., Hu C., and MacKenzie C., “High-Dimensional Reliability Analysis of Engineered Systems Involving Computationally Expensive Black-Box Simulations,” ASME International Design Engineering Technical Conferences & Computers and Information in Engineering Conference (IDETC/CIE), Aug 6-9 2017, Cleveland, OH. [ DOI ]
10. Li Z., Wu D., Hu C., Terpenny J., and Shen S., “Ensemble Prognostics with Degradation-Dependent Weights: Prediction of Remaining Useful Life for Aircraft Engines,” ASME International Design Engineering Technical Conferences & Computers and Information in Engineering Conference (IDETC/CIE), Aug 6-9 2017, Cleveland, OH.  [ DOI ]
11. Sadoughi M., Hu C., and MacKenzie C., “A Maximum Expected Utility Method for Efficient Reliability Analysis of Complex Engineered Systems,” 18th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, 2017 AIAA AVIATION Forum, Jun 5–9 2017, Denver, CO.  [ DOI ]
12. Li Z., Jiang Y., Hu C., and Peng Z., “Multi-Dimensional Variational Mode Decomposition Applied to Intrinsic Vibration Mode Extraction for Bearing Crack Detection in Wind Turbines with Large Speed Variation,” 35th Wind Energy Symposium, 2017 AIAA SciTech Forum, Jan 9-13 2017, Grapevine, TX.  [ DOI ]